Il teorema della palla pelosa e la circolazione generale dell’atmosfera
Di Claudio Giulianelli
Leggendo il titolo, o meglio, il nome del teorema esilarante, potreste pensare che sia uno scherzo. Questo articolo non vuole essere una descrizione precisa e rigorosa di un teorema matematico ma piuttosto uno spunto di riflessione per poi spingere i più curiosi verso questo argomento a fare ulteriori ricerche personali. Il teorema della palla pelosa (il cui nome in termini matematici verrà spiegato successivamente) è un punto di partenza nella descrizione del funzionamento della nostra atmosfera, delle sue fondamenta. Potremmo effettivamente dire che è fondamentale nella descrizione del funzionamento dell’atmosfera.
Partiamo analizzando il nome del teorema.
I matematici definiscono “palla” un qualunque oggetto di forma circolare,indipendentemente dalla dimensione che lo caratterizza. Si parla quindi di palla n-dimensionale. Ad esempio abbiamo il cerchio,il disco,la sfera e così via fino a infinite dimensioni. Tutti questi oggetti si riassumono sotto il nome di palla. Pelosa…in realtà per pelosa non c’è una definizione matematica, per fortuna oserei dire! La scelta di questo aggettivo sarà chiara spiegando il teorema.
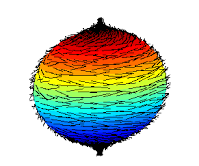
Con questo teorema si vuole dimostrare che comunque si pettini una palla letteralmente pelosa, ci si troverà sempre di fronte a punti in cui la disposizione dei peli non è più continua,ma cambia in modo discontinuo. Nel caso dell’atmosfera per esempio, se si assimila la sfera ad un pianeta e la si pettina da sinistra verso destra, troveremo due singolarità, corrispondenti a due poli (prima immagine sotto). Da questo se ne può dedurre dunque che qualunque pianeta che ruoti su se stesso (dunque con atmosfera sempre in movimento,altrimenti non ci sarebbero singolarità e nulla da pettinare),presenta nella circolazione generale atmosferica due grandi ruote depressionarie,il cui centro è il polo.
Se vogliamo questa è la spiegazione matematica del perché esiste la fascia climatica del vortice polare, che racchiude tutto il serbatoio gelido che si può disperdere alle medie latitudini in inverno. Questo teorema esemplifica la circolazione generale dell’atmosfera, dove i peli sono i vettori che rappresentano la velocità del vento sulla superficie del pianeta. Vento che matematicamente viene visto dunque come campo vettoriale.
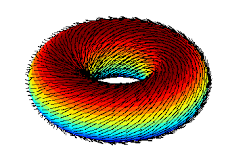
Nella seconda immagine invece abbiamo un toro, il quale può essere pettinato senza presentare singolarità. Su un pianeta che abbia quella forma dunque non esisterebbero vortici,se non per la presenza di rilievi, ma i moti dell’aria rimarrebbero costanti nel tempo.