3) Fluidodinamica, le equazioni di Eulero e la vorticità: la fluidodinamica ancora non ben compresa
di Emanuele Santinami
L’equazione di Eulero, che abbiamo derivato nel precedente articolo, rappresenta il punto di partenza nello studio dei fluidi.
Ad esso è associata la cosiddetta equazione di continuità, che ha questa formulazione matematica, derivabile dal principio di conservazione della massa.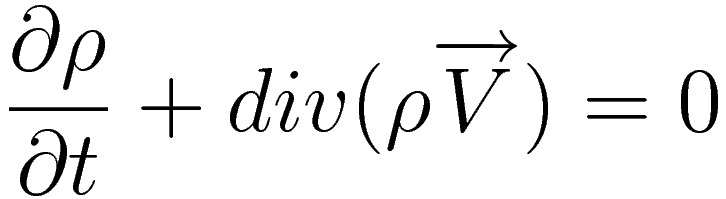
Essa stabilisce un po’ le “regole del gioco” del nostro sistema: non ci sono pozzi o sorgenti che alterano la quantità totale di fluido, ma il sistema ha una quantità fissa di fluido.
Una grande semplificazione è richiedere che il fluido sia incomprimibile, cioè che la densità del fluido sia costante (le palline di fluido sono tutte equispaziate, non si schiacciano mai in un punto). Questa ipotesi è certamente vera nei liquidi, che sono appunto incomprimibili, ma anche in buona parte dei casi, nei gas (un’eccezione a questo è rappresentata ad esempio nella formazione di un temporale, a cui sono associate zone di bassa pressione e una convergenza del vento, tuttavia in questo caso interverrebbero altre variabili come la temperatura e non siamo più in condizione di usare ragionamenti semplificati come fatti fin’ora).
Imponendo quindi che la densità sia costante, che si traduce nella condizione di derivata nel tempo della densità pari a 0 e nell’uscita della densità dal simbolo di divergenza, otteniamo che la divergenza del campo di velocità è nulla, che è una cosa assolutamente ragionevole: non ci sono punti di divergenza/convergenza, i puntini di fluido infatti non si schiacciano né si allontanano da alcun punto.
Ricordiamoci che l’equazione di Eulero è in realtà formata da tre equazioni, una per ogni componente, aggiungendo l’equazione di continuità abbiamo a che fare già con quattro equazioni. Queste equazioni sono già molto complicate e non sono risolvibili carta e penna, almeno allo stato attuale delle cose. Le opzioni sono due: ricorrere a metodi numerici, facendole risolvere al computer, o provare a semplificarle, supponendo di trovarci in determinate condizioni, potendo così trascurare dei termini delle equazioni.
Discuteremo ora alcuni tentativi con questa seconda strada.
Un’approssimazione molto comune nell’atmosfera è quella del cosiddetto bilancio idrostatico, e nasce dall’osservazione, abbastanza ragionevole, del fatto che i moti zonali (sul piano orizzontale xy) siano molto più importanti della componente verticale (lungo z); in altre parole, supponiamo che moti verticali di vento siano trascurabili (e questo, ad esempio, è giusto a parte di trovarci dentro un cumulonembo, che ha notevoli venti convettivi al suo interno). Ciò matematicamente consente di semplificare molti termini dell’equazione in z, in cui la diminuzione di pressione lungo la direzione z cresce linearmente all’aumentare della quota (sappiamo che più si sale e più diminuisce la pressione dell’aria).
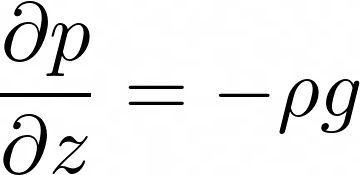
Introduciamo ora un concetto chiave nello studio dei fluidi: la vorticità. La definizione matematica non è molto intuitiva, ma diciamo che è la capacità di un campo di vento (o di qualsiasi altro fluido) di generare moti rotatori.

Così come la divergenza quantifica quanto il fluido tende a convergere o divergere da un punto, l’operatore matematico che quantifica la vorticità in un punto si chiama rotore del campo di velocità: se in una certa zona è diverso da zero, in quel punto c’è vorticità, ossia vi è un cambio di direzione nella linea del flusso; se è uguale a zero, in tale zona il campo si dice irrotazionale.
Passiamo ad una prima applicazione dell’equazione di Eulero, il cosiddetto Teorema di circolazione di Kelvin. Consideriamo una qualsiasi traiettoria chiusa (per esempio un anello), in una zona qualsiasi del fluido. Questo anello ideale viene trasportato nel fluido e può deformarsi (un po’ come una matassa di polline trasportata nell’aria, o il fumo di una sigaretta).

Procediamo a studiare la circolazione d’aria di questo anello, al variare del tempo. Si tratta di studiare matematicamente la seguente quantità:
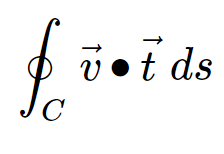
Effettuando il conto, includendo in esso l’equazione di Eulero, arriviamo al risultato che questa circolazione non cambia nel tempo. Nel dimostrare questo importante risultato, noto come teorema di Kelvin, non possiamo immediatamente usare l’equazione di Eulero perché l’anello su cui integriamo può deformarsi, ma avendo cura di assicurarsi che alcuni dettagli matematici della questione siano ininfluenti, si prova effettivamente che tale conto ci dice che la circolazione in un anello di fluido non cambia nel tempo a causa delle equazioni di Eulero che contengono solo forze conservative, nella fattispecie il gradiente di pressione. Il gradiente di pressione è una forza irrotazionale, analogamente al campo elettrico che si diffonde in maniera radiale attorno la carica sorgente che lo genera, o al campo gravitazionale. Il teorema di Stokes ci dice che tale integrale lungo l’anello equivale al flusso del rotore di tale forza. Ma se la forza è irrotazionale, ha rotore nullo. Abbiamo dunque capito che nel fluido così descritto da Eulero il fatto che questo conservi l’energia ha come conseguenza che se guardassimo il moto dell’acqua lungo qualsiasi linea chiusa ci venga in mente, questo non cambierebbe durante il tragitto.
Vediamo di interpretare questo risultato.
Facciamo ora la seguente osservazione: dal teorema di Kelvin abbiamo che la circolazione non cambia nel tempo e sarà pari ad un valore, costante. Per il teorema di Stokes allora anche il flusso del rotore della velocità attraverso tale anello non cambia nel tempo, e sarà pari ad un certo valore, costante. Possiamo dire quindi che il rotore della velocità sia un certo valore, costante. Troviamo espressi matematicamente questi passaggi sotto:
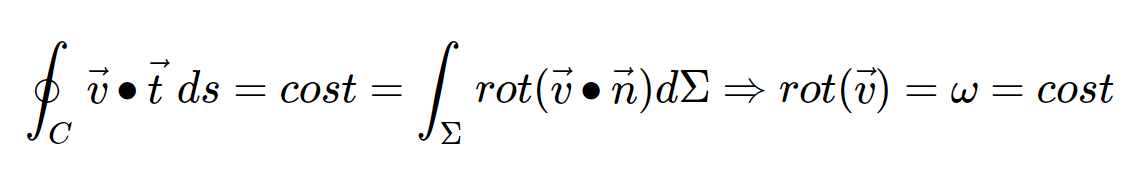
Ora immaginiamo di guardare un flusso d’acqua che si muove in maniera uniforme che va contro un ostacolo, una palla. Un flusso d’acqua dunque in partenza senza vortici e turbolenze, ossia un flusso d’acqua dove non c’è rotazione, nessun mulinello. Matematicamente vuol dire un fluido con rotore nullo (scegliamo dunque la costante, omega, pari a 0). Dal teorema di Kelvin deduciamo che se la descrizione della fluidodinamica di Eulero è corretta, allora tale valore del rotore non cambia nel tempo. Vuol dire che il fluido ignora la presenza della palla, in ogni punto continua a non mostrare rotazioni ne prima ne durante ne dopo l’interazione con la palla. Stiamo dicendo che l’aria non ha avuto nessuna interazione con l’oggetto, ma ci scorre intorno. E questo è vero sia per l’aria, quanto per l’acqua e qualsiasi altro tipo di fluido in ogni contesto. In questo modo nello spazio tridimensionale non potrebbero esistere né portanza né traino. Gli aerei non volerebbero, il vento non avrebbe modo di muovere niente, così come una secchiata d’acqua ci scivolerebbe addosso senza nemmeno spostarci. Questo risultato assurdo prende il nome di paradosso di D’Alambert.
La risoluzione di questo problema non è da ricercare nei passaggi matematici, che sono rigorosi, quanto in una nostra scarsa comprensione del fenomeno fisico. C’è qualcosa che ci sfugge, ed è la forza di attrito (proprio quella che viene costantemente trascurata). In effetti, l’equazione di Eulero nuda e cruda contiene solo le forze di pressione e nient’altro, nemmeno la forza di gravità (che possiamo includere “a mano” ad esempio con l’ipotesi di bilancio idrostatico). La forza di attrito è la vera responsabile dell’interazione del fluido con la materia, mediante un trasferimento di energia dal fluido, che perde quantità di moto, a qualsiasi oggetto, che la acquista, o viceversa.
Al di là di questa situazione, malgrado la loro semplicità, le equazioni di Eulero sono in grado di dare spiegazione a molti fenomeni. Ad esempio, se il fluido ha un moto stazionario, cioè il flusso non cambia nel tempo, e ha vorticità nulla, possiamo inserire queste ipotesi nelle equazioni di Eulero, semplificandole molto (derivata di V rispetto al tempo uguale a zero, e rotore di V uguale a zero). Fatto ciò, rimaniamo con il seguente termine che risulta essere costante nello spazio.
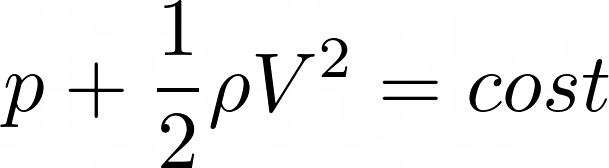
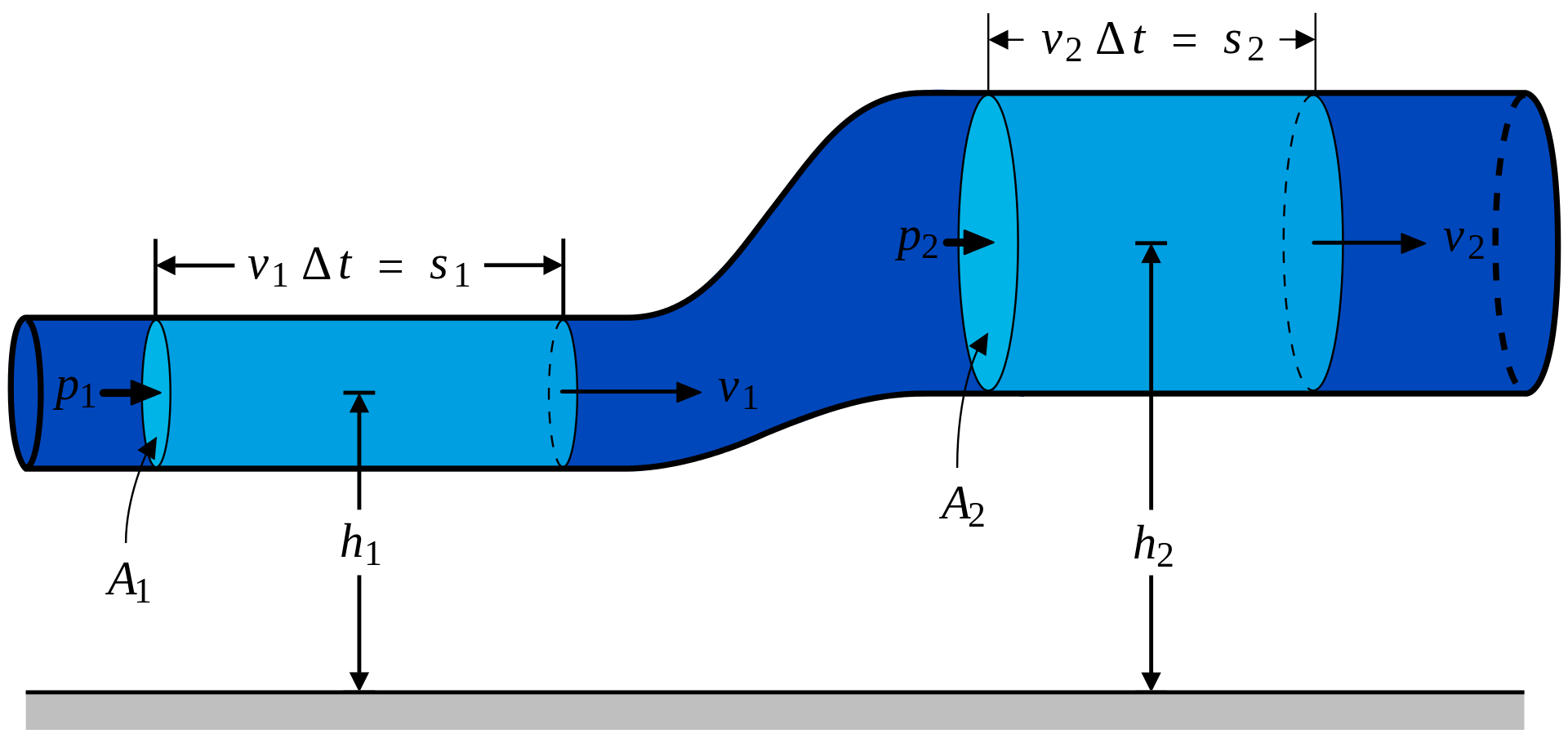
Abbiamo ricavato la famosa equazione di Bernoulli, che mette in relazione pressione, densità e velocità di un fluido (e si può specializzare ulteriormente includendo anche il termine ρgh). Essa rappresenta l’analogo della legge di conservazione dell’energia meccanica applicata ai fluidi ed è di grandissima utilità pratica perché risulta applicabile in molti contesti con buona approssimazione: ad esempio, accoppiando questa equazione con l’equazione di continuità, specializzata al caso di flussi in canali e tubature (velocità x superficie = costante, cioè in ogni sezione del tubo il flusso di fluido è costante), permette di risolvere molti problemi di questo tipo, oppure che in generale la pressione di un fluido diminuisce all’aumentare della sua velocità. Questo è cruciale ad esempio per capire cos’è la portanza e come volano gli aerei: in grande sintesi, il profilo stondato della parte superiore dell’ala consente all’aria di avere una maggiore velocità sopra di essa, e quindi una pressione inferiore; di conseguenza l’aria sotto all’ala tenta di compensare allo squilibrio di pressione spingendola verso l’alto.
Normalmente, al liceo l’equazione di Bernoulli viene ricavata in maniera più semplice dal teorema dell’energia cinetica e da altre considerazioni, ma il fatto che un sistema di equazioni differenziali alle derivate parziali possa ricondursi con semplicità allo stesso risultato, sotto opportune ipotesi, è una prova di quanto sia robusta e valida la teoria dietro all’equazione di Eulero.